Segitiga Pascal dan Ekspansi Binomium Newton

MEMAHAMI INTERVAL KECEKUNGAN

7055

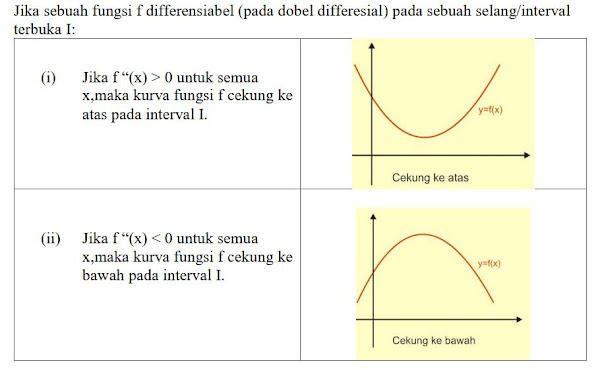
MODEL OGIVE GARIS ATAU KURVATURE

Pada materi statistika, dalam pembahasan model penyajian data kita akan berhadapan dengan produk yang dinamakan "Grafik Frekuensi Kumulatif" atau yang dikenal pula dengan nama "Ogive", baik "Ogive Positif" maupun "Ogive Negatif". Yang menjadi bahan refleksi dan akan dikembangkan untuk dicermati para siswa adalah tentang bagaimana cara membuat produk Ogive tersebut. APAKAH GRAFIKNYA DENGAN GARIS? APAKAH GRAFIKNYA DENGAN GARIS LENGKUNG (KURVATURE)? Dalam dunia ilmiah, kita selalu merujuk kepada apa yang telah ada sebagi sumber acuan. Artinya apapun yang kita lakukan, asalkan ada sumber rujukannya, maka kite diperbolehkan menggunakan rujukan tersebut. Khusus kali ini, kita melihat beberapa buku sumber dan produk yang ada di dalamnya :

6910

LOGIKA MATEMATIKA

A.  PERNYATAAN (STATEMENT) DAN BUKAN PERNYATAAN

Untuk memahami pengertian pernyataan, silakan ikuti gambaran ini :

1.    Jika ada orang mengatakan “ 5 + 34 = 39”  , maka bagi orang yang telah belajar matematika akan merespon bahwa hal tersebut adalah BENAR .

2.    Jika ada orang mengatakan “ Lagu kebangsaan Indonesia adalah Kimigayo”  , maka bagi orang yang telah belajar akan merespon bahwa hal tersebut adalah SALAH .

3.    Jika ada orang bertanya “ Siapa namamu Nak ?”  , maka bagi orang yang telah belajar akan merespon bahwa hal tersebut adalah tidak BENAR tidak juga SALAH..

4.    Jika ada orang menyampaikan ajakan  “Mari kita maju bersama !” , maka bagi orang yang telah belajar akan merespon bahwa hal tersebut adalah tidak BENAR tidak juga SALAH .

Pada contoh (1) dan (2) , karena kita dapat merespon BENAR (B) atau SALAH (S) maka contoh tersebut dinamakan PERNYATAAN. Sedangkan untuk nomor nomor (3) dan (4) dinamakan BUKAN PERNYATAAN . Dalam suatu pernyataan tidak mungkin mengandung dua buah nilai B atau S secara bersamaan. Nilai B atau S yang merupakan senuah respon dari suatu pernyataan disebut nilai kebenaran ( truth) . Notasi nilai kebenaran adalah t (tau) . Misalnya suatu pernyataan p jika memaksudkan nilai kebenaran p akan ditulis t (p). Contoh yang lain misalkan nilai kebenaran dari ~p Ú q akan ditulis t (~p Ú q), dan seterusnya.

Yakinkan pemahananmu dengan melihat tabel berikut :

No	Kalimat / Fakta	Pernyataan/Bukan	B / S
1	Jakarta merupakan kota metropolitan	Pernyataan	B
2	Benarkah 42 – 3 < 10 ?	Bukan pernyataan	-
3	42 – 3 < 10	Pernyataan	S
4	Jika x2 = 6 maka x = Ö6	Pernyataan	S
5	Jika x2 = 6 maka x = Ö6 atau x = -Ö6	Pernyataan	B
6	Mari kita mulai rapat ini !	Bukan pernyataan	-

 

Jika  terdapat suatu pernyataan yang kebenarannya harus dibuktikan terlebih dahulu, atau nilai kebenarannya tergantung kapan sesesorang menyatakannya, pernyataan ini disebut pernyataan fakultatif.

Contoh 1        :

1.    Hari ini udara cerah .

Misalnya sesorang siswa membaca catatan tersebut pada hari yang cerah maka nilai kebenarannya adalah Benar (B), tetapi jika siswa tersebut membaca pada malam hari ketika sedang belajar, maka jawaban B tidak tepat.

2.    Besok hari Senin.

Jika orang yang menyatakan kalimat tersebut pada hari Minggu, maka yang ia ucapkan menjadi pernyataan yang benar, tetapi jika mengucapkannya hari Rabu, maka akan menjadi pernyataan yang salah.

 

 

B.  TABEL KEBENARAN

 

Tabel kebenaran (The Truth Table) merupakan alat yang digunakan untuk memberikan nilai dengan aturan tertentu . Tabel kebenaran digunakan oleh Gottlob Frege ketika mengembangkan teori Boole tentang fungsi kebenaran (elective function).

Tabel kebenaran digunakan untuk menjelaskan secara sistematis nilai-nilai kebenaran dari proposisi-proposisi sederhana, seperti prosisi tunggal (atomic) dan proposisi majemuk .

 

C.  NEGASI ( INGKARAN ) SUATU PERNYATAAN

Dari setiap pernyataan akan dapat ditentukan pernyataan lain yang mempunyai nilai kebenaran berlawanan dengan nilai kebenaran pernyataan semula. Pernyataan baru ini dinamakan Ingkaran atau Negasi dari pernyataan pertama .

Notasi Ingkaran : Jika pernyataan semula diberikan sebagai p maka ingkarannya diberi notasi ~ p atau Ø p

 

      Tabel kebenaran Ingkaran :

	p	~ p	Dalam menyatakan ingkaran dikenal beberapa kata-kata ingkar (ciri ingkar) di antaranya :  bukan, tidak, tidak benar bahwa
	B	S
	S	B

 

	Notasi ingkar untuk tanda hubung matematika
	p	~ p
	>	≤
	<	≥
	≥	<
	≤	>
	=	≠

 

D. TABEL KEBENARAN PERNYATAAN MAJEMUK

KONJUNGSI				IMPLIKASI
p	Q	p Ù q	Ciri khas konjungsi: “Menang S-nya”	p	Q	p ® q	Ciri khas implikasi: B®S nilai S (Salah) Selain itu B (benar)
B	B	B		B	B	B
B	S	S		B	S	S
S	B	S		S	B	B
S	S	S		S	S	B
DISJUNGSI				BIIMPLIKASI
p	Q	p Ú q	Ciri khas disjungsi : “Pilih yang B (baik)”	p	Q	p Û q	Ciri khas biimplikasi: Jika kembar, B Jika beda, S
B	B	B		B	B	B
B	S	B		B	S	S
S	B	B		S	B	S
S	S	S		S	S	B

  

E. NEGASI PERNYATAAN MAJEMUK

 

No	Negasi - Pola	Pernyataan dan negasinya
1	~ (p Ù q) º ~ p Ú ~ q	Pernyataan:  Itik merupakan unggas dan gajah bukan mamalia.
		Negasi       :  Itik bukan merupakan unggas atau gajah merupakan mamalia.
2	~ (p Ú q) º ~ p Ù ~ q	Pernyataan :  2 > 0 atau  Ö4 = 2
		Negasi        : 2 ≤ 0 dan Ö4 ≠ 2
3	~ (p® q) º p Ù ~ q	Pernyataan     :  Jika saya malas maka orang tua khawatir.
		Negasi            : Saya malas dan orang tua tidak khawatir

 

   F. EKUIVALENSI

No	Equivalensi	Implikasi dan ekuivalensin a
1	p® q º ~ q ®  ~ p	Implikasi : Jika saya lulus, maka saya akan mentraktir teman. Pernyataaan yang ekuivalen / setara / senilai ditulis dengan 2 (dua) model yakni model 1 dan model 2. Jadi jawabannya adalah : 1.      Jika saya tidak akan mentraktir teman maka saya tidak lulus. 2.      Saya tidak lulus atau mentraktir teman.
2	p® q º ~ p Ú q

 

G. KONVERS, INVERS DAN KONTRAPOSISI

     Konvers, invers dan kontraposisi berkaitan dengan suatu implikasi.

No	Model	Nama	Contoh
1	p® q	Implikasi	Jika KPK beraksi maka koruptor tidak berkutik
2	q® p	Konvers	Jika koruptor tidak berkutik maka KPK beraksi
3	~ p® ~q	Invers	Jika KPK tidak beraksi maka koruptor berkutik
4	~ q® ~ p	Kontraposisi	Jika koruptor berkutik maka KPK tidak beraksi

 H. KUANTOR DAN NEGASI KUANTOR

      Pernyataan dalam bentuk kalimat berkuantor merupakan kalimat yang di dalamnya mengandung pengertian “berapa banyak”                                             

1.        Kuantor Universal  , modelnya : ("xÎS).(P(x)) , dibaca “Untuk setiap x anggota S, maka berlakulah P(x)”.

2.        Kuantor Eksistensial, modelnya :  ($xÎS).(P(x)) , dibaca “Beberapa x anggota S, maka berlakulah P(x)”.

     Negasi kuantor :

             ~  ("xÎS).(P(x))  adalah   ($xÎS).( ~P(x) )

             ~  ($xÎS).(P(x))   adalah  ("xÎS).( ~P(x) )

I. PENARIKAN KESIMPULAN (YANG SAH)

================================

SOAL LATIHAN PEMAHAMAN

1.	Kontraposisi dari pernyataan majemuk p → ( p Ú ~q ) adalah ….
	a.	(pÚ~q)→~p			d.	(~pÚq)→~p
	b.	(~pÙq)→~p			e.	(pÙ~q)→~p
	c.	(pÚ~q)→p
2.	Diketahui premis-premis :  (1) Jika Siti sakit maka dia pergi ke dokter                                     (2) Jika Siti pergi ke dokter maka dia diberi obat. Kesimpulan yang sah dari argumen tersebut adalah ….
	a.	Siti tidak sakit dan tidak diberi obat			d.	Siti tidak sakit atau tidak diberi obat
	b.	Siti sakit dan diberi obat			e.	Siti tidak sakit atau diberi obat
	c.	Siti sakit atau diberi obat
3.	Diketahui argumentasi : I.                                      II.                            III.                                          Argumentasi yang sah adalah ….
	a.	I saja			d.	I dan II
	b.	II saja			e.	II dan III
	c.	III saja
4.	Pernyataan yang salah adalah ….
	a. Ö92 = Ö32  atau (Ö3)2 = Ö92
	b. Jika x2 - 1 = 24 maka x =  5 atau x = - 5
	c. Jika ikan hidup di air, maka harimau bukan binatang buas.
	d. log 1000 = 3 dan log 3 = 1000
	e. Jika emas bukan logam maka Hari Anti Pembabatan Hutan akan dicanangkan pada 17 November 2016
5,	Jika ~p bernilai salah (S) , q bernilai benar (B) dan  r bernilai salah (S) , maka pernyataan yang bernilai salah (S) adalah ….
	a.	(pÚ~r)Þq			d.	(~pÙr)Þ(pÚ~r)
	b.	(pÙ~q)Ú~r			e.	(~qÚr)Þ~p
	c.	(pÞr) Ù (rÞ~q)
6.	Negasi dari : “Para siswa  mengerti dan tidak bingung” adalah ….
	a.	Para siswa tidak mengerti tetapi bingung
	b.	Para siswa mengerti tetapi tidak bingung
	c.	Para siswa tidak mengerti atau bingung
	d.	Para siswa tidak bingung atau mengerti
	e.	Para siswa tidak mengerti tetapi bingung
7.	Negasi dari “ Jika kamu tidak suka maka sayapun tidak suka” adalah ….
	a.	Jika kamu suka maka sayapun suka
	b.	Jika kamu suka maka saya tidak suka
	c.	Kamu tidak suka dan saya suka.
	d.	Kamu tidak suka atau saya suka.
	e.	Kamu suka dan saya tidak suka.
8.	Nilai kebenaran dari : (p Ù (~q Þ ~p)) Þ q adalah ….
	a.	BBBS			d.	BSSS
	b.	BBSB			e.	BBBB
	c.	BBSS
9.	Pernyataan : “Jika Bagus mendapat hadiah maka ia senang” setara dengan ….
	a.	Jika Bagus tidak senang maka ia tidak mendapat hadiah
	b.	Bagus mendapat hadiah tetapi ia tidak senang
	c.	Bagus mendapat hadiah dan ia senang
	d.	Bagus tidak mendapat hadiah atau ia tidak senang
	e.	Bagus tidak senang dan ia tidak mendapat hadiah
10.	Diberikan premis-premis: Premis 1   : Jika hari Senin bertanggal genap maka upacara bendera diadakan Premis 2   : Jika upacara bendera diadakan maka guru matematika bertindak sebagai pembina upacara Premis 3   : Guru matematika tidak bertindak sebagai pembina upacara Kesimpulan yang sah ….
	a.	Hari Senin bertanggal genap
	b.	Hari Senin tidak bertanggal genap
	c.	Upacara bendera tetap diadakan
	d.	Upacara bendera tidak diadakan
	e.	Upacara bendera berlangsung khidmat
11.	Diberikan premis-premis: Premis 1   : Jika panen melimpah maka penghasilan petani meningkat Premis 2   : Jika penghasilan petani meningkat maka mereka makmur Premis 3   : Petani tidak makmur Kesimpulan yang sah ….
	a.	Penghasilan petani tidak meningkat
	b.	Penghasilan petani menurun
	c.	Panen tidak melimpah
	d.	Petani tidak panen
	e.	Petani gagal panen
12.	Diberikan premis-premis: Premis 1   : Jika harga BBM naik maka harga sembako naik Premis 2   : Jika harga sembako naik maka tarif tol naik Premis 3   : Tarif tol tidak naik Kesimpulan yang sah ….
	a.	Jika harga BBM naik maka tarif tol naik
	b.	Jika harga sembako naik maka tarif tol naik
	c.	Harga BBM naik
	d.	Harga BBM tidak naik
	e.	Harga sembako tidak naik
13.	Pernyataan : “Jika kendaraan bermotor menggunakan bahan bakar gas maka tingkat polusi udara dapat diturunkan”. Pernyataan yang setara adalah ….
	a.	Kendaraan bermotor menggunakan bahan bakar gas dan tingkat polusi udara tidak dapat diturunkan
	b.	Kendaraan bermotor tidak menggunakan bahan bakar gas atau tingkat polusi udara dapat diturunkan
	c.	Kendaraan bermotor tidak menggunakan bahan bakar gas dan tingkat polusi udara dapat diturunkan
	d.	Jika tingkat polusi udara dapat diturunkan maka kendaraan bermotor menggunakan bahan bakar gas
	e.	Jika tingkat polusi udara tidak dapat diturunkan maka kendaraan bermotor menggunakan bahan bakar gas
		UN 2013 – barcode era
14.	Jika Adi tidak sombong maka Adi mempunyai banyak teman. Pada kenyataaannya Adi tidak mempunyai banyak teman. Kesimpulan yang benar adalah ….
	a.	Adi pasti sombong
	b.	Adi mungkin anak yang baik
	c.	Adi bukan anak yang baik
	d.	Adi punya beberapa teman
	e.	Adi anak yang baik
15.	Ingkaran dari “Tiada orang menyukai matematika” adalah ….
	a.	Semua orang menyukai matematika
	b.	Beberapa orang tidak menyukai matematika
	c.	Beberapa orang ada yang tidak menyukai matematika
	d.	Beberapa orang menyukai matematika
	e.	Semua orang tidak suka matematika
						Tes Masuk Undip 2009
16.	Negasi dari pernyataan “Semua siswa menganggap matematika sukar” adalah ….
	a.	Beberapa siswa menganggap matematika sukar
	b.	Semua siswa menganggap matematika sukar
	c.	Ada siswa menganggap  matematika tidak sukar
	d.	Tidak seorangpun siswa menganggap matematika sukar
	e.	Ada siswa tidak menganggap matematika mudah
		Tes Masuk STT Telkom 2009
17.	Jika (~pÚq) bernilai salah dan p®r bernilai salah, maka pernyataan berikut yang bernilai salah adalah ….
	a.	pÙq			d.	q®p
	b.	pÚq			e.	r®p
	c.	pÚr				Tes Masuk STT Telkom 2009
18.	Diketahui fakta : “Seluruh peserta Try-Out sedang berfikir”. (1)  Jika Tukul peserta Try-Out maka ia sedang berfikir. (2) Jika Sule bukan peserta Try-Out maka ia tidak sedang berfikir. (3) Jika Untung sekarang tidak sedang berfikir, maka ia bukan peserta Try-Out (4) Jika Kasino sekarang sedang berfikir, maka ia peserta Try-Out     Pernyataan yang benar adalah ….
	a.	(1), (2)	b.	(1), (3)	c.	(2), (4)	d.	(1),(3),(4)	e.	Hanya (1)
19.	Pernyataan yang setara dengan “ Jika semua sekolah menyelenggarakan upacara hari Senin, maka semua siswa lebih mencintai tanah airnya. “ adalah ……
	a.	Beberapa sekolah tidak menyelenggarakan upacara hari Senin atau semua siswa lebih mencintai tanah airnya.
	b.	Ada siswa yang tidak mencintai tanah airnya dan ada sekolah yang tidak menyelenggarakan upacara hari Senin.
	c.	Ada sekolah yang menyelenggarakan upacara hari Senin da nada siswa yang lebih mencintai tanah airnya.
	d.	Semua siswa mencintai tanah airnya dan semua sekolah menyelenggarakan upacara hari Senin.
	e.	Semua siswa tidak mencintai tanah airnya atau se,mua sekolah tidak menyelenggarakan upacara pada hari Senin.
										UN 2015
20.	Diketahui : Premis 1 : Ayah tidak ke rumah sakit atau ayah periksa ke dokter. Premis 2 : Ayah tidak periksa ke dokter. Kesimpulannya adalah ….
	a.	Ayah ke rumah sakit
	b.	Ayah tidak ke rumah sakit
	c.	Ayah di rumah saja
	d.	Ayah tidak ke rumah sakit dan ayah tidak periksa ke dokter.
	e.	Ayah ke rumah sakit dan ayah tidak periksa ke dokter.
										UN 2015

 

6695