Tuntutlah ilmu dari ayunan hingga liang lahat. Pendidikan sepanjang hayat, atau pendidikan dari nol hingga nol.Semua istilah kadang menjadi begitu berbeda di dalam pengamalannya. Ilmu hanya menjadi pengetahuan yang tak tembus ke hati, tak nyata dalam amalan. "Ada yang salah dalam pendidikan kita!" Benar! Sebagai akibat, tentu "Ada yang benar dalam pendidikan kita." Ada, tapi tentu dalam proporsi mayoritas. Ya, kebenaran harus mayoritas! Kita harus optimis.
Assalaamu'alaikum!
Selasa, 23 Maret 2021
Minggu, 21 Maret 2021
PERTIDAKSAMAAN NILAI MUTLAK
Istilah:
“Nilai Mutlak” memiliki istilah lain yang sama artinya yaitu “Harga Mutlak” atau "Harga Absolut" atau “Modulus”.
Notasi :
Notasi nilai mutlak adalah “ | ….. |”
Contoh cara membaca:
1. |2| dibaca “Nilai mutlak dari 2” atau “Harga mutlak dari 2”
2. |-7| dibaca “Nilai mutlak dari -7” atau “Harga mutlak dari -7”
3. | x – 4 | dibaca “Nilai mutlak dari x – 4 “ atau “Harga mutlak dari x – 4 “
Nilai mutlak sesungguhnya adalah terkait dengan “jarak” , yakni sebuah nilai yang selalu membuat sesuatu yang berada di antara notasi “ | ….. |” menjadi positif.
Fungsi nilai mutlak :
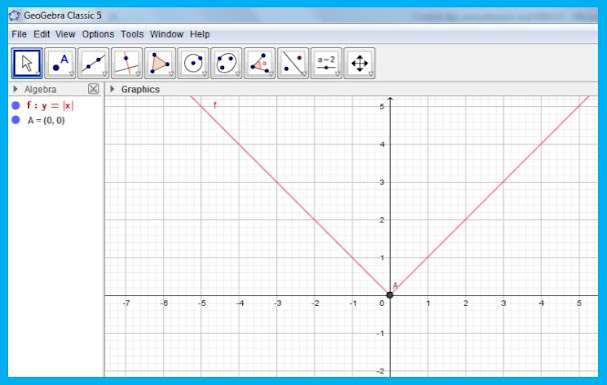
Grafiknya :
Grafik dibuat dengan aplikasi Geogbra.
Dari grafik tersebut tampak bahwa:
1. 1. |-5| = 5
2. 2. |-4|= 4
3. 3. |0| = 0
4. 4. |3| =3
5. 5. |5| = 5 , dan sebagainya.
Dengan demikian dapat dikembangkan pemahamannya bahwa :
1. 1. |6 - 9 | = |-3| = 3
2. 2. |12 - 7| = |5| = 5 , dan sebagainya.
Contoh 1:
Sifat : “Untuk a > 0 , jika |x| ≥ a , maka x ≤ - a atau x ≥ a”
Jika |x – 6| ≥ 5 maka interval yang memenuhi adalah ….
A. A. 1 ≤ x ≤ 11
B. B. - 11 ≤ x ≤ - 1
C. C. x ≤ - 5 atau x ≥ 5
D. D. x ≤ 1 atau x ≥ 11
E. E. x ≤ - 1 atau x ≥ 11
Jawab:
| x – 6| ≥ 5 → x – 6 ≤ – 5 atau x – 6 ≥ 5
(i) x – 6 ≤ – 5
x ≤ 6 – 5 ……………………perhatikan perpindahan posisi “ – 6 ” menjadi “6”
x ≤ 1
(ii) x – 6 ≥ 5
x ≥ 6 + 5 ......…………………perhatikan perpindahan posisi “ – 6 ” menjadi “6”
x ≥ 11
Penyelesaian x ≤ 1 atau x ≥ 11
Himpunan penyelesaian {x| x ≤ 1 atau x ≥ 11} → Opsi (D)
Contoh 2 :
Sifat : “Untuk a > 0 , jika |x| ≥ a , maka x ≤ - a atau x ≥ a”
Jika |4x – 1| ≥ 7 maka interval yang memenuhi adalah ….
Contoh 3:
Sifat : “Untuk a > 0 , jika |x| ≤ a , maka - a ≤ x ≤ a”
Jika | x + 7| ≤ 12 maka interval x yang memenuhi adalah ….
A. A. – 5 ≤ x ≤ 5
B. B. – 19 ≤ x ≤
C. C. – 12 ≤ x ≤ 12
D. D. x ≤ – 19 atau x ≥ 5
E. E. x ≤ – 5 atau x ≥ 19
Jawab :
| x + 7| ≤ 12 → – 12 ≤ x + 7 ≤ 12
– 12 ≤ x + 7 ≤ 12 → – 12 – 7 ≤ x ≤ 12 – 7 ……. Perhatikan “–7” berpindah ruas di dua tempat.
– 12 – 7 ≤ x ≤ 12 – 7
– 19 ≤ x ≤ 5
Penyelesaian – 19 ≤ x ≤ 5
Himpunan penyelesaian {x| – 19 ≤ x ≤ 5 } → Opsi (B)
Untuk pertidaksamaan ingatlah :
Contoh :
Tentukan penyelesaian dari 2x2 + 11 x – 6 ≥ 0
Jawab :
2x2 + 11 x – 6 ≥ 0
(2x – 1)(x + 6) ≥ 0
i) Harga nol
2x – 1 = 0 → x = ½
x + 6 = 0 → x = - 6
ii) Pindahkan x = ½ dan x = - 6 ke dalam garis bilangan
iii) Pilih salah satu nilai x (asalkan bukan harga nol), kemudian substitusikan ke model
(2x – 1)(x + 6) untuk memperoleh tanda hasil “– “ atau “ + “ . Hasilnya pindahkan
ke garis bilangan. Lengkapi tanda berselang-seling setiap kali melewati batas.
Pilih x = 0
Untuk (2x – 1)(x + 6) maka (2(0) – 1)(0 + 6) = (-1)(6) = - 6 (tanda negatif)
iv) Memilih daerah
Karena soal 2x2 + 11 x – 6 ≥ 0 (maka pilih daerah ≥ 0 atau yang bertanda “+”)
Jawab untuk soal :
2x2 + 11 x – 6 ≥ 0 maka penyelesaiannya x ≤ - 6 atau x ≥ ½ .
Contoh 4 :
Tentukan penyelesaian dari |2x + 1| ≥ |x – 3|
Jawab :
· Sifat yang digunakan “Untuk |x| ≥ |a| maka x2 ≥ a2 “
|2x + 1| ≥ |x – 3| → (2x + 1)2 ≥ (x – 3)2
(2x + 1)2 – (x – 3)2 ≥ 0
[(2x + 1) – (x – 3)].[ (2x + 1) + (x – 3)] ≥ 0
[2x + 1 – x + 3].[ 2x + 1 + x – 3] ≥ 0
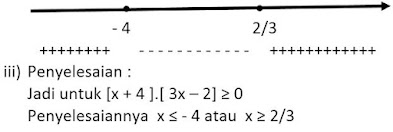
[x + 4 ].[ 3x – 2] ≥ 0
i) Harga nol x = - 4 dan x = 2/3
ii) Garis bilangan :
PERSAMAAN
NILAI MUTLAK
Pertidaksamaan mengandung variabel dan tanda / notasi : >, < , ≥ atau ≤ , sedangkan pada persamaan tanda hubungnya adalah “sama dengan” atau “ =”.
Sifat yang
digunakan adalah model fungsi dasar dan sifat ketiga.
Contoh 5 :
Tentukan
penyelesaian dari | - 3x | - 18 = 0
Jawab:
| - 3x | - 18
= 0
| - 3x | = 18
|-3|.|x| = 18
3.|x| = 18
|x| = 18/3
|x|= 6,
Sehingga penyelesaiannya x = - 6 atau x = 6
Contoh 6 :
Tentukan
penyelesaian dari |x – 2|+ 3 = 15
Jawab:
|x – 2|+ 3 = 15
|x – 2| = 15 –
3
|x – 2| = 12
Untuk model
ini diperoleh dua buah akibat:
yaitu x – 2 = – 12 dan x – 2 = 12
(i)
Untuk x – 2 = – 12 → x = – 10
(ii)
Untuk x – 2 = 12 → x = 14
Sehingga penyelesaiannya x = – 10 atau x = 14
Contoh
7 :
Carilah himpunan penyelesaian dari |x + 1| + 3 = 2x
Jawab :
Cara 1 (Menggunakan yang mirip sifat 3 pada pertidaksamaan)
|x + 1| + 3 = 2x
|x + 1| = 2x – 3 kemudian
dikuadratkan kiri dan kanan.
(x + 1)2 = (2x – 3)2
(x + 1)2 – (2x – 3)2 = 0
[(x + 1) – (2x – 3)]. [(x
+ 1) + (2x – 3)]=0
[ x + 1 – 2x + 3].[ x + 1 + 2x – 3] = 0
(– x + 4)(3x – 2) = 0
(i)
Untuk – x + 4
= 0 → x = 4
(ii)
Untuk 3x – 2 = 0 → x =
2/3
Sehingga penyelesaiannya x = 4 atau x = 2/3
Cara 2 (mengkuadratkan biasa ruas kiri dan ruas kanan)
|x + 1| + 3 = 2x
|x + 1| = 2x – 3 kemudian
dikuadratkan kiri dan kanan.
(x + 1)2 = (2x – 3)2
(x + 1)2 – (2x – 3)2 = 0
x2
+ 2x + 1 – [4x2 – 12x + 9] = 0
x2
+ 2x + 1 – 4x2 + 12x – 9 = 0
– 3x2
+ 14x – 8 = 0
3x2 – 14x + 8 = 0
kemudian bentuk ini difaktorkan sesuai dengan cara yang dipelajari di SMP/MTs.
(3x
– 2)(x – 4) = 0
(i)
Untuk 3x – 2 =0 → x = 2/3
(ii)
Untuk x – 4 = 0 → x =
Sehingga penyelesaiannya x = 4 atau x = 2/3
SELAMAT BELAJAR
Majalengka, Maret 2021
41772