Edukasi dan Fiksi: UJI HIPOTESIS - PENARIKAN KESIMPULAN

Materi penarikan kesimpulan berkaitan dengan uji hipotesis, sifatnya hanya pengenalan dasar. Persyaratan normalitas data yang dikenakan pada data yang diuji telah dibahas pada topik distribusi normal. Akan tetapi tidak sampai pada uji normalitas menggunakan metode tertentu.

Kondisi kenormalan data pada populasi dikenalkan melalui grafik fungsi densitas peluang, untuk melihat grafik yang diperoleh. Tentang data riil berdistribusi normal dapat dilihat melalui link https://www.youtube.com/watch?v=5fyojHO1JZc atau juga khusus untuk melihat data dengan fungsi densitas peluang pada link https://www.youtube.com/watch?v=2AGQEZ02dTE.

HIPOTESIS

Penarikan kesimpulan yang dipelajari di SMA untuk memberikan gambaran pada saat di pendidikan tinggi berhubungan langsung dengan kegiatan penelitian ilmiah dengan bantuan statistika. Penelitian yang dilakukan umumnya untuk melakukan sebuah prediksi hasil tertentu dari sesuatu yang dirancang dan akan diuji dengan statistika. Prediksi atau dugaan inilah yang dimaksudkan dengan hipotesis.

Dari arti katanya, hipotesis berasal dari 2 penggalan kata, “hypo” yang artinya “di bawah” dan “thesa” yang artinya kebenaran. Ketika cara penulisannya disesuaikan dengan ejaan Bahasa Indonesiamenjadi “hipotesa”, dan berkembang menjadi “hipotesis” (Arikunto, 2006).

Contoh hipotesis di dunia pendidikan yang bisa dilakukan oleh peneliti misalnya:

· Metode belajar daring meningkatkan prestasi belajar siswa.

· Pemberian PR yang banyak akan meningkatkan ketahanan belajar.

· Terdapat korelasi positif antara harga HP dengan hasil ujian.

Hipotesis semacam ini sengaja dibuat oleh peneliti untuk diuji bahwa yang diprediksi adalah benar secara statistik.

Beberapa pengertian hipotesis dari berbagai sumber:

(1) Hipotesis merupakan suatu proposisi / pernyataan atau jawaban sementara/ dugaan yang mungkin benar dan digunakan sebagai pembuatan keputusan / penyelesaian dari suatu masalah penelitian (Kadir, 2010)

(2) Hipotesis adalah hasilkajian pustaka atau proses rasional dari proses penelitian yang telah mempunyai kebenaran teoretik. Kebenaran hipotesis masih harus diuji kebenarannya secara empiric, dengan demikian hipotesis dapat dianggap sebagai jawaban sementara terhadap masalah yang telah dirumuskan dalam suatu penelitian dan masih perlu diuji kebenarannya dengan menggunakan data empirik (Djaali 2003, dalam Kadir, 2010).

(3) Hipotesis diartikan sebagai kesimpulan bersifat sementara atau proposisi tentative tentang hubungan antara dua variabel atau lebih (Kerlinger 2002, dalam Kadir, 2010).

(4) Hipotesis adalah pernyataan atau dugaan tentang karakter suatu populasi yang masih lemah kebenarannya dan perlu dibuktikan (Noormandiri,2017)

(5) Hipotesis dapat diartikan sebagai suatu jawaban yang bersifat sementara terhadap permasalahan penelitian, sampai terbukti melalui data yang terkumpul (Arikunto, 2006).

Uji hipotesis yang dipilih di materi SMA adalah uji Z. Terkait dengan uji Z ini maka dikaitkan proses pengambilan kesimpulan dengan kurva normal. Uji ini melihat posisi pada daerah-daerah mana hasil uji diperoleh,beradadi daerah H₀ataukah berada di daerah H₁.

MODEL UJI HIPOTESIS dan KRITERIA PENGUJIAN

Dengan asumsi bahwa data populasi berdistribusi normal, sehingga yang dijadikan patokan sebagai sebuah hasil penarikan kesimpulan terhadap hipotesis adalah dengan bantuan kurva normal.

Terdata dua macam model uji hipotesis yang disesuaikan dengan penentuan hipotesis nol, yakni uji hipotesis satu arah dan uji hipotesis dua arah.

Pada bagian ini khusus untuk uji mean :

a. a. Uji hipotesis satu arah (sepihak / one tail)

b. Uji hipotesis dua arah (dua pihak / two tail)

MENENTUKAN SIGNIFIKANSI

Level atau taraf signifikan yang merupakan besar toleransi penerimaan persentase kesalahan hasil hipotesis.

Level siginifikan yang lazim digunakan adalah 1%, 5%, 10%. Persentase ini masih bisa dimodifikasi sesuai dengan arah atau posisi daerah penolakan H₀.

· (1) Jika level signifikan 1% maka derajat kepercayaannya 99%.

· (2) Jika level signifikan 5% maka derajat kepercayaannya 95%.

· (3) Jika level signifikan 10% maka derajat kepercayaannya 90%.

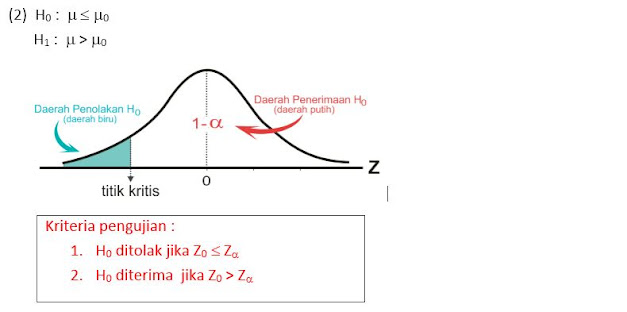
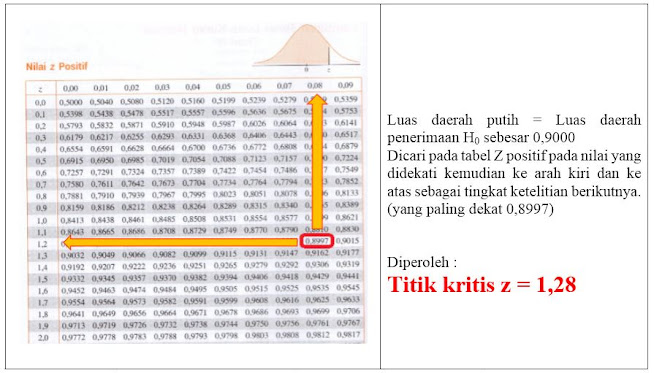
TITIK KRITIS

Titik kritis dapat pula disebut nilai kritis pada uji Z dengan bantuan kurva normal merupakan nilai z batas antara daerah penerimaan H₀ dengan daerah penolakan H₀(H₁).

a. aa a. Titik Kritis 1% untuk Uji One Tail (satu pihak) arah kanan

b. Titik Kritis 5% untuk Uji One Tail (satu pihak) arah kanan

c. Titik Kritis 10 % untuk Uji One Tail (satu pihak) arah kanan

Untuk uji arah kiri, posisi daerah biru simetris di sebelah kiri nilai z = 0 sehingga karena luas sama berbeda posisi, tinggal ditambahkan tanda “negatif” padasetiap nilai kritis uji arah kanan.

Dari ketiga proses tersebut dapat dilihat bahwa :