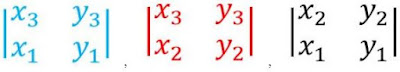Menghitung
luas segitiga?
Ini
sebuah hal yang sederhana, namun siapa tahu ada hal baru yang belum anda
peroleh.
Misalkan
diketahui sebuah segitiga ABC yang diketahui titik-titik sudut
A(1,1), B (5,2) dan C(4,6).
Apa saja yang dibutuhkan untuk menghitung luas segitiga tersebut?
Jawabannya mungkin :
1. “panjang masing-masing sisi”
2. Diagram Cartesius.
3. ...
4. ...
atau apa saja yang terlintas dalam pikiran kita terhadap apa-apa yang pernah dipelajari.
5 CARA MENGHITUNG LUAS SEGITIGA
Berikut
ini 5 (lima) cara menghitung luas segitiga (L) tersebut di atas:
Nah, itulah lima cara menghitung luas daerah segitiga di atas.
Hitung-hitung review untuk diri, maupun ketika adik-adik Anda, atau putra/putri Anda perlu referensi bisa saja dipakai.
Terutama untuk cara kelima menggunakan trik determinan matriks, mungkin cara ini belum populer, atau tidak populer, bisa saja. Tetapi saya pribadi malah enak menggunakan cara ini jika diminta menghitung luas daerah segitiga sembarang yang diketahui ketiga titik sudutnya.
Sumbangan
SUPLEMEN PENJELAS CARA 5
Pokok pikiran utamanya
sama dengan CARA
3 adalah bahwa:
Luas segitiga ABC (L)
: L = Luas APQR – L1 – L2
– L3
Luas segitiga ABC (L)
:
L = Luas
APQR – L1 – L2 – L3 atau
L = Luas APQR – (L1
+ L2 + L3)
(i) Hitung terlebih
dahulu p = L1 + L2 + L3
p=( x3 y2 – x3
y3 – x2 y2 + x2 y3
) +
( x3 y3 – x3
y1 – x1 y3 + x1 y1
) +
( x2 y2 – x2
y1 – x1 y2 + x1 y1
)
= ( x3 y2
– x3 y3 – x2 y2 +
x2 y3 + x3 y3
– x3 y1 – x1 y3 +
x1 y1 + x2 y2
– x2 y1 – x1 y2 +
x1 y1 )
= ( x3 y2
+ x2 y3 – x3 y1 – x1
y3 + x1 y1 – x2 y1 – x1
y2 + x1 y1 )
= ( x3 y2
+ x2 y3 – x3 y1 – x1
y3 – x2 y1 – x1 y2
+ 2 x1 y1 )
(ii) Hitung luas:
L =
Luas APQR – (L1 + L2 + L3)
= (x3 y2
– x3 y1 –
x1 y2 + x1 y1) –
( x3 y2 + x2 y3
– x3 y1 – x1 y3
– x2 y1 – x1
y2 + 2 x1 y1 )
= x3 y2
– x3 y1 –
x1 y2 + x1 y1 –
x3 y2
–
x2
y3 +
x3 y1 +
x1
y3 +
x2 y1 +
x1
y2 – x1 y1
=
x3 y2 –
x3 y2 – x3 y1
+
x3 y1
–
x1 y2 +
x2 y1 + x1 y1
–x1 y1 –
x2
y3 +
x1
y3 +
x1
y2
=
x3 y2 –
x3 y1
–
x2 y1 –
x2
y3 +
x1
y3 +
x1
y2
=
( x3 y2 –
x3 y1 –
x2
y1 –
x2
y3 +
x1
y3 +
x1
y2 )
=
( x3 y2
– x3 y1 –
x2
y1 –
x2 y3 +
x1 y3 +
x1
y2 )
=
( x3 y2
–
x2 y3) – x3 y1
+
x1 y3 –
x2
y1 +
x1
y2 )
=
( (x3 y2
–
x2 y3) + (
x1 y3 – x3 y1)
+
x1
y2 – x2 y1 ) )
=
((x3 y2
–
x2 y3) –
(x3 y1 –x1 y3) +
x2
y1 – x1 y2 ) )
KETERANGAN TAMBAHAN:
Melihat urutan
variabel berindeks dengan pola keteraturan indeks (yang besar di atas) untuk model matriks ordo 3 x 3
determinannya:
Dengan melihat hasil tersebut tampak bahwa :
merupakan determinan matriks minor (M) - nya.
Dengan ekspansi pada
cofactor (Cij) untuk i = baris dan j = kolom , formula yang ada :
maka
:
Jadi untuk segitiga
sembarang
dengan titik sudut (x1,y1), (x2,y2)
dan (x3,y3) adalah :
Catatan khusus:
(1) Model untuk rumus L tidak tergantung pada rumus pertama yang sudah diuraikan asal muasalnya. Akan tetapi bisa bervariasi pada setiap baris matriksnya. Jika anda masih ingat permutasi susunan baris dalam rumus, maka banyaknya model matriks terdapat sebanyak 3! (tiga faktorial) = 6 model (6 rumus L).
(2) Jika dalam hal terdapat kasus koordinat mengandung bilangan negatif, rumus tetap berlaku.
(3) Jika kasus yang dihadapi adalah muncul bilangan bertanda negatif, maka tinggal diberi nilai mutlak untuk mendapatkan nilai "Luas" yang positif.
Sumbangan dari Majalengka Jawa Barat
SMA Negeri 1 Majalengka
765