Istilah:
“Nilai Mutlak” memiliki istilah lain yang sama artinya yaitu “Harga Mutlak” atau "Harga Absolut" atau “Modulus”.
Notasi :
Notasi nilai mutlak adalah “ | ….. |”
Contoh cara membaca:
1. |2| dibaca “Nilai mutlak dari 2” atau “Harga mutlak dari 2”
2. |-7| dibaca “Nilai mutlak dari -7” atau “Harga mutlak dari -7”
3. | x – 4 | dibaca “Nilai mutlak dari x – 4 “ atau “Harga mutlak dari x – 4 “
Nilai mutlak sesungguhnya adalah terkait dengan “jarak” , yakni sebuah nilai yang selalu membuat sesuatu yang berada di antara notasi “ | ….. |” menjadi positif.
Fungsi nilai mutlak :
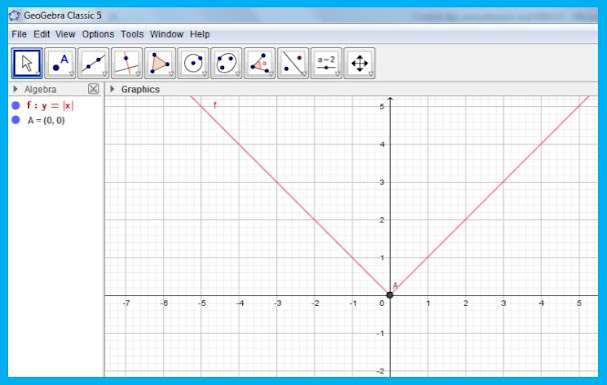
Grafiknya :
Grafik dibuat dengan aplikasi Geogbra.
Dari grafik tersebut tampak bahwa:
1. 1. |-5| = 5
2. 2. |-4|= 4
3. 3. |0| = 0
4. 4. |3| =3
5. 5. |5| = 5 , dan sebagainya.
Dengan demikian dapat dikembangkan pemahamannya bahwa :
1. 1. |6 - 9 | = |-3| = 3
2. 2. |12 - 7| = |5| = 5 , dan sebagainya.
Contoh 1:
Sifat : “Untuk a > 0 , jika |x| ≥ a , maka x ≤ - a atau x ≥ a”
Jika |x – 6| ≥ 5 maka interval yang memenuhi adalah ….
A. A. 1 ≤ x ≤ 11
B. B. - 11 ≤ x ≤ - 1
C. C. x ≤ - 5 atau x ≥ 5
D. D. x ≤ 1 atau x ≥ 11
E. E. x ≤ - 1 atau x ≥ 11
Jawab:
| x – 6| ≥ 5 → x – 6 ≤ – 5 atau x – 6 ≥ 5
(i) x – 6 ≤ – 5
x ≤ 6 – 5 ……………………perhatikan perpindahan posisi “ – 6 ” menjadi “6”
x ≤ 1
(ii) x – 6 ≥ 5
x ≥ 6 + 5 ......…………………perhatikan perpindahan posisi “ – 6 ” menjadi “6”
x ≥ 11
Penyelesaian x ≤ 1 atau x ≥ 11
Himpunan penyelesaian {x| x ≤ 1 atau x ≥ 11} → Opsi (D)
Contoh 2 :
Sifat : “Untuk a > 0 , jika |x| ≥ a , maka x ≤ - a atau x ≥ a”
Jika |4x – 1| ≥ 7 maka interval yang memenuhi adalah ….
Contoh 3:
Sifat : “Untuk a > 0 , jika |x| ≤ a , maka - a ≤ x ≤ a”
Jika | x + 7| ≤ 12 maka interval x yang memenuhi adalah ….
A. A. – 5 ≤ x ≤ 5
B. B. – 19 ≤ x ≤
C. C. – 12 ≤ x ≤ 12
D. D. x ≤ – 19 atau x ≥ 5
E. E. x ≤ – 5 atau x ≥ 19
Jawab :
| x + 7| ≤ 12 → – 12 ≤ x + 7 ≤ 12
– 12 ≤ x + 7 ≤ 12 → – 12 – 7 ≤ x ≤ 12 – 7 ……. Perhatikan “–7” berpindah ruas di dua tempat.
– 12 – 7 ≤ x ≤ 12 – 7
– 19 ≤ x ≤ 5
Penyelesaian – 19 ≤ x ≤ 5
Himpunan penyelesaian {x| – 19 ≤ x ≤ 5 } → Opsi (B)
Untuk pertidaksamaan ingatlah :
Contoh :
Tentukan penyelesaian dari 2x2 + 11 x – 6 ≥ 0
Jawab :
2x2 + 11 x – 6 ≥ 0
(2x – 1)(x + 6) ≥ 0
i) Harga nol
2x – 1 = 0 → x = ½
x + 6 = 0 → x = - 6
ii) Pindahkan x = ½ dan x = - 6 ke dalam garis bilangan
iii) Pilih salah satu nilai x (asalkan bukan harga nol), kemudian substitusikan ke model
(2x – 1)(x + 6) untuk memperoleh tanda hasil “– “ atau “ + “ . Hasilnya pindahkan
ke garis bilangan. Lengkapi tanda berselang-seling setiap kali melewati batas.
Pilih x = 0
Untuk (2x – 1)(x + 6) maka (2(0) – 1)(0 + 6) = (-1)(6) = - 6 (tanda negatif)
iv) Memilih daerah
Karena soal 2x2 + 11 x – 6 ≥ 0 (maka pilih daerah ≥ 0 atau yang bertanda “+”)
Jawab untuk soal :
2x2 + 11 x – 6 ≥ 0 maka penyelesaiannya x ≤ - 6 atau x ≥ ½ .
Contoh 4 :
Tentukan penyelesaian dari |2x + 1| ≥ |x – 3|
Jawab :
· Sifat yang digunakan “Untuk |x| ≥ |a| maka x2 ≥ a2 “
|2x + 1| ≥ |x – 3| → (2x + 1)2 ≥ (x – 3)2
(2x + 1)2 – (x – 3)2 ≥ 0
[(2x + 1) – (x – 3)].[ (2x + 1) + (x – 3)] ≥ 0
[2x + 1 – x + 3].[ 2x + 1 + x – 3] ≥ 0
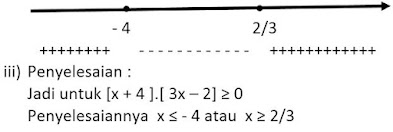
[x + 4 ].[ 3x – 2] ≥ 0
i) Harga nol x = - 4 dan x = 2/3
ii) Garis bilangan :
PERSAMAAN
NILAI MUTLAK
Pertidaksamaan mengandung variabel dan tanda / notasi : >, < , ≥ atau ≤ , sedangkan pada persamaan tanda hubungnya adalah “sama dengan” atau “ =”.
Sifat yang
digunakan adalah model fungsi dasar dan sifat ketiga.
Contoh 5 :
Tentukan
penyelesaian dari | - 3x | - 18 = 0
Jawab:
| - 3x | - 18
= 0
| - 3x | = 18
|-3|.|x| = 18
3.|x| = 18
|x| = 18/3
|x|= 6,
Sehingga penyelesaiannya x = - 6 atau x = 6
Contoh 6 :
Tentukan
penyelesaian dari |x – 2|+ 3 = 15
Jawab:
|x – 2|+ 3 = 15
|x – 2| = 15 –
3
|x – 2| = 12
Untuk model
ini diperoleh dua buah akibat:
yaitu x – 2 = – 12 dan x – 2 = 12
(i)
Untuk x – 2 = – 12 → x = – 10
(ii)
Untuk x – 2 = 12 → x = 14
Sehingga penyelesaiannya x = – 10 atau x = 14
Contoh
7 :
Carilah himpunan penyelesaian dari |x + 1| + 3 = 2x
Jawab :
Cara 1 (Menggunakan yang mirip sifat 3 pada pertidaksamaan)
|x + 1| + 3 = 2x
|x + 1| = 2x – 3 kemudian
dikuadratkan kiri dan kanan.
(x + 1)2 = (2x – 3)2
(x + 1)2 – (2x – 3)2 = 0
[(x + 1) – (2x – 3)]. [(x
+ 1) + (2x – 3)]=0
[ x + 1 – 2x + 3].[ x + 1 + 2x – 3] = 0
(– x + 4)(3x – 2) = 0
(i)
Untuk – x + 4
= 0 → x = 4
(ii)
Untuk 3x – 2 = 0 → x =
2/3
Sehingga penyelesaiannya x = 4 atau x = 2/3
Cara 2 (mengkuadratkan biasa ruas kiri dan ruas kanan)
|x + 1| + 3 = 2x
|x + 1| = 2x – 3 kemudian
dikuadratkan kiri dan kanan.
(x + 1)2 = (2x – 3)2
(x + 1)2 – (2x – 3)2 = 0
x2
+ 2x + 1 – [4x2 – 12x + 9] = 0
x2
+ 2x + 1 – 4x2 + 12x – 9 = 0
– 3x2
+ 14x – 8 = 0
3x2 – 14x + 8 = 0
kemudian bentuk ini difaktorkan sesuai dengan cara yang dipelajari di SMP/MTs.
(3x
– 2)(x – 4) = 0
(i)
Untuk 3x – 2 =0 → x = 2/3
(ii)
Untuk x – 4 = 0 → x =
Sehingga penyelesaiannya x = 4 atau x = 2/3
SELAMAT BELAJAR
Majalengka, Maret 2021
41772